|
|

By Dr. Leila Gonzalez
(and friends)
|
Note: This is a reprint of an article that originally appeared in the LA Times on April 8, 1999.
What is all this fuss about
spinning? As we have seen, a simple question such as “How do
skaters get spinning so fast?” is not so simple. Many of you
figured out that skaters bring their arms in to speed up, and this
explains “how” but not “why.” So, this week,
let’s take a look at “why!”
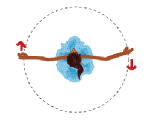 The top
down views of the skater summarize what you found out. The first skater
(right) has her arms extended and the short arrows indicate that she is spinning
slowly.
The top
down views of the skater summarize what you found out. The first skater
(right) has her arms extended and the short arrows indicate that she is spinning
slowly.
When the same skater (as shown in
the second drawing, below) holds her arms closer to her body, she spins faster,
as indicated by the longer arrows. The arrows represent the
“rotational velocity” with longer arrows representing a faster
spin. Physicists use the symbol w for rotational velocity.
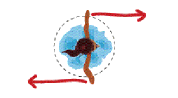 What these diagrams show you is that
the way the body is distributed has a large effect on the spinning
speed. To describe this, physicists talk about something called
“rotational inertia” and use the symbol I. Inertia is the
tendency for a body to resist a change in motion. Spinning objects that
are spread out will resist change more than compact objects. In other
words, the more spread out an object is, the higher its rotational
inertia. Objects that are more compact have low rotational inertia and
are able to change more easily.
What these diagrams show you is that
the way the body is distributed has a large effect on the spinning
speed. To describe this, physicists talk about something called
“rotational inertia” and use the symbol I. Inertia is the
tendency for a body to resist a change in motion. Spinning objects that
are spread out will resist change more than compact objects. In other
words, the more spread out an object is, the higher its rotational
inertia. Objects that are more compact have low rotational inertia and
are able to change more easily.
When we combine rotational velocity
and rotational inertia by multiplying them together (represented as Iw),
we have defined angular momentum. Using this definition, we can show
why skaters spin faster with their arms close to their bodies. As I
mentioned in a previous article, the key to understanding the change in
the skater’s speed is the Law of Conservation of Angular Momentum.
An object’s angular momentum is conserved, unless an outside force
acts on the object.
Because of this conservation, if
we change one part of angular momentum, the other part has to change.
So, if the skater moves her arms closer to her body, both the rotational
velocity and rotational inertia change, but in opposite directions.
As the arms come in, rotational
inertia decreases and rotational velocity increases, making the skater
spin faster. But, if she puts her arms out, her rotational inertia
increases, which decreases her rotational velocity and slows her
down.
So, now that you have an equation
that describes how the skater controls spin, how can you apply this to
the frozen fruit can experiment? Next week I will publish answers to
that question, and you may be surprised. (I was!)
|
|